Generating Chunks

Core logic for generating chunks:

async function generateChunks(bundle, getHashPlaceholder) {
  const {
    experimentalMinChunkSize,
    inlineDynamicImports,
    manualChunks,
    preserveModules
  } = this.outputOptions;
  const manualChunkAliasByEntry =
    typeof manualChunks === 'object'
      ? await this.addManualChunks(manualChunks)
      : this.assignManualChunks(manualChunks);
  const snippets = getGenerateCodeSnippets(this.outputOptions);
  const includedModules = getIncludedModules(this.graph.modulesById);
  const inputBase = commondir(
    getAbsoluteEntryModulePaths(includedModules, preserveModules)
  );
  const externalChunkByModule = getExternalChunkByModule(
    this.graph.modulesById,
    this.outputOptions,
    inputBase
  );
  const chunks = [];
  const chunkByModule = new Map();
  for (const { alias, modules } of inlineDynamicImports
    ? [{ alias: null, modules: includedModules }]
    : preserveModules
      ? includedModules.map(module => ({ alias: null, modules: [module] }))
      : getChunkAssignments(
          this.graph.entryModules,
          manualChunkAliasByEntry,
          experimentalMinChunkSize,
          this.inputOptions.onLog
        )) {
    // Sort modules by execIndex (execution order) from smallest to largest
    sortByExecutionOrder(modules);
    const chunk = new Chunk(
      modules,
      this.inputOptions,
      this.outputOptions,
      this.unsetOptions,
      this.pluginDriver,
      this.graph.modulesById,
      chunkByModule,
      externalChunkByModule,
      this.facadeChunkByModule,
      this.includedNamespaces,
      alias,
      getHashPlaceholder,
      bundle,
      inputBase,
      snippets
    );
    chunks.push(chunk);
  }
  for (const chunk of chunks) {
    chunk.link();
  }
  const facades = [];
  for (const chunk of chunks) {
    facades.push(...chunk.generateFacades());
  }
  return [...chunks, ...facades];
}

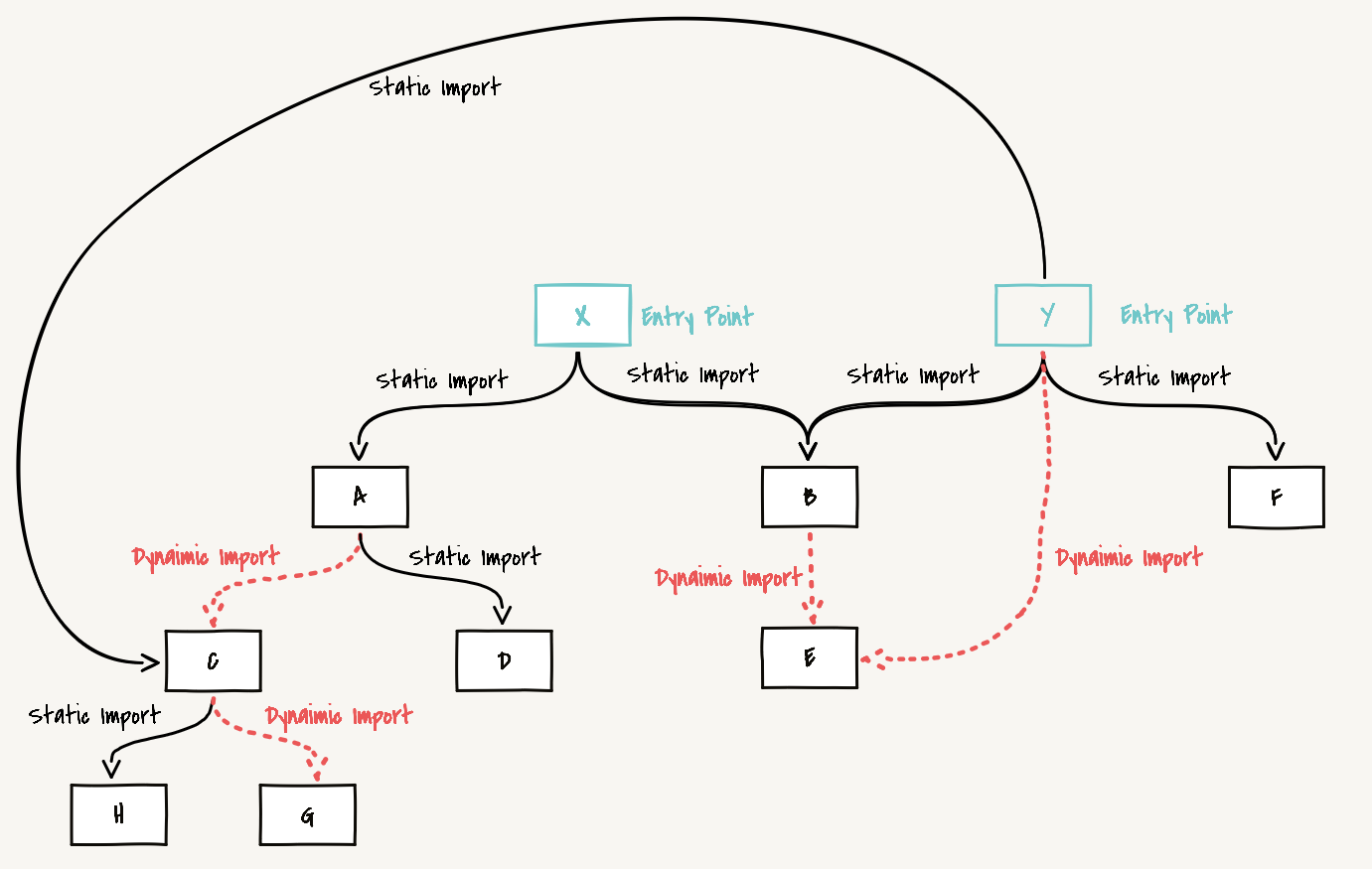
Example, assuming the dependency graph relationship is as follows:

Rollup configuration:

// rollup.config.js
export default {
  input: {
    X: './X.js',
    Y: './Y.js'
  },
  output: [
    {
      dir: 'dist/esm',
      format: 'es',
      entryFileNames: '[name].js',
      manualChunks: {
        common1: ['D'],
        common2: ['C', 'F']
      }
    }
  ],
  treeshake: false,
  plugins: []
};

Given the above example scenario, we can understand the implementation principles of chunk in the following sections.

Processing Manual Chunk Logic

Different handling for two different parameter passing methods: object and function

const manualChunkAliasByEntry =
  typeof manualChunks === 'object'
    ? await this.addManualChunks(manualChunks)
    : this.assignManualChunks(manualChunks);

Through the above method, we can obtain a structure of Map<Module, string>, representing the custom chunk name corresponding to each module. This is just a layer of mapping and retrieval, without any merging logic. It's worth noting that if a module doesn't exist in the dependency graph, we need to call the fetchModule method again to get the latest module object.

Since generating chunks happens in the await bundle.generate(isWrite); phase, meaning the dependency graph has already been built, if the custom module is a subset of the dependency graph, we can directly use the cached parsed module.

The resulting structure would be:

// rollup configuration
const rollupConfig = {
  manualChunks: {
    common1: ['./D.js'],
    common2: ['./C.js', './F.js']
  }
};

// final result
const manualChunkAliasByEntry = {
  ModuleD: 'common1',
  ModuleC: 'common2',
  ModuleF: 'common2'
};

Then in the getChunkDefinitionsFromManualChunks method, we use addStaticDependenciesToManualChunk to perform a BFS traversal under the following conditions:

if (
  !(
    dependency instanceof ExternalModule ||
    modulesInManualChunks.has(dependency)
  )
) {
  modulesToHandle.add(dependency);
}

And add them to modulesInManualChunks. This means that modulesInManualChunks will record all manually chunked modules and their non-external module static dependency modules.

const chunkDefinitions = [
  {
    alias: 'common1',
    modules: [ModuleD]
  },
  {
    alias: 'common2',
    modules: [ModuleC, ModuleG, ModuleF]
  }
];

const modulesInManualChunks = new Set([ModuleD, ModuleC, ModuleF, ModuleG]);

Analyzing Dependency Graph

In the analyzeModuleGraph(entries) method, we use the user-configured entry points as the starting points for BFS traversal, in this case X and Y modules. Through BFS traversal of all entry modules, we collect the correspondence between modules and entry modules. It's worth noting that if a module is dynamically loaded in a static module, when a dynamic module dependency is detected, the dynamic dependency module is added to allEntries as a new entry module, waiting for subsequent BFS traversal. Through relationship determination, we can finally obtain four data structures: allEntries, dependentEntriesByModule, dynamicallyDependentEntriesByDynamicEntry, and dynamicImportsByEntry. Let's explain these four data structures one by one.

1. allEntries

   All entry modules, including user-defined entry modules and dynamic modules. In this example, we can get:

   const allEntries = [ModuleX, ModuleY, ModuleC, ModuleE, ModuleH];

   C, E, H are dynamic modules, which are added to allEntries as new entry modules during BFS traversal when dynamic module dependencies are detected.

2. dependentEntriesByModule

   Stores the mapping relationship between all modules (including user-defined entry modules and dynamic modules) and their corresponding dependent entry module indices.

   Entry Module Index Explanation

   • 0 corresponds to entry module ModuleX
   • 1 corresponds to entry module ModuleY
   • 2 corresponds to dynamic module ModuleC
   • 3 corresponds to dynamic module ModuleE
   • 4 corresponds to dynamic module ModuleH

   const dependentEntriesByModule = new Map([
     [ModuleX, new Set([0])],
     [ModuleA, new Set([0])],
     [ModuleB, new Set([0, 1])],
     [ModuleD, new Set([0])],
     [ModuleY, new Set([1])],
     [ModuleC, new Set([1, 2])],
     [ModuleF, new Set([1])],
     [ModuleG, new Set([1, 2])],
     [ModuleE, new Set([3])],
     [ModuleH, new Set([4])]
   ]);

   Brief Explanation

   • From the dependency graph in the example, we can see that ModuleX, ModuleY, ModuleC, ModuleE, ModuleH are all entry modules, so their dependent entry module indices are 0, 1, 2, 3, 4.
   • For ModuleB, there are two reachable entry modules, ModuleX and ModuleY, so its dependent entry module indices are 0, 1.
   • ModuleC is itself a dependency module entry, and also serves as a static dependency of ModuleY, so its dependent entry module indices are 1, 2.
   • ModuleG is the only static dependency of ModuleC, so its dependent entry modules are the same as ModuleC, which is 1, 2.

3. dynamicallyDependentEntriesByDynamicEntry

   Establishes the mapping relationship between the entry index of a dynamic module and the dependent entry module indices of its dynamic module dependents.

   const dynamicallyDependentEntriesByDynamicEntry = new Map([
     [2, new Set([0])],
     [3, new Set([0, 1])],
     [4, new Set([1, 2])]
   ]);

   Brief Explanation

   • From the dependency graph in the example, we can see that ModuleC is loaded as a dynamic dependency by ModuleA, and ModuleA's dependent entry module is ModuleX, so the mapping relationship is [2(Module C's entry module index), {0(Module X's entry module index)}].
   • Similarly, ModuleE is loaded as a dynamic dependency by ModuleB and ModuleY. ModuleB's dependent entry modules are ModuleX and ModuleY, and ModuleY's dependent entry module is ModuleY, so the union is {0, 1}, and the mapping relationship is [3(Module E's entry module index), {0(Module X's entry module index), 1(Module Y's entry module index)}].
   • Similarly, ModuleH is loaded as a dynamic dependency by ModuleC. ModuleC's dependent entry modules are ModuleC and ModuleY, so the mapping relationship is [4(Module H's entry module index), {1(Module Y's entry module index), 2(Module C's entry module index)}].

4. dynamicImportsByEntry

   Stores the mapping relationship between all entry modules and their corresponding dynamic dependency modules that need to be loaded.

   const dynamicImportsByEntry = new Map([
     [0, new Set([2, 3])],
     [1, new Set([4])]
   ]);

   Brief Explanation

   • In all paths where ModuleX is the entry module, the dynamic modules that need to be loaded are ModuleC (X → A → C) and ModuleE (X → B → E).
   • In all paths where ModuleY is the entry module, the dynamic modules that need to be loaded are ModuleE (Y → E) and ModuleC (Y → C). Note that ModuleE is already a dynamic dependency module of ModuleX, so it's not added again here.

   for (const [entryIndex, entry] of allEntries.entries()) {
     entryIndexByModule.set(entry, entryIndex);
     if (dynamicEntryModules.has(entry)) {
       dynamicEntries.add(entryIndex);
     }
   }

Merging Modules into Chunks

const chunkAtoms = getChunksWithSameDependentEntries(
  getModulesWithDependentEntries(
    dependentEntriesByModule,
    modulesInManualChunks
  )
);

1. Filter out all dependency modules contained in custom chunks

   From the implementation of getModulesWithDependentEntries, we can see that the modules fed to getChunksWithSameDependentEntries will not include any modules in modulesInManualChunks. This means that all dependency modules contained in custom chunks will not be packaged in other chunks later.

   function* getModulesWithDependentEntries(
     dependentEntriesByModule,
     modulesInManualChunks
   ) {
     for (const [module, dependentEntries] of dependentEntriesByModule) {
       if (!modulesInManualChunks.has(module)) {
         yield { dependentEntries, modules: [module] };
       }
     }
   }

2. Merging Modules into chunks

   In getChunksWithSameDependentEntries, we use chunkSignature (i.e., whether they have the same entry module dependencies) to determine if two modules can be merged. If two modules have the same chunkSignature, it means these two modules can be merged into the same chunk.

   function getChunksWithSameDependentEntries(modulesWithDependentEntries) {
     const chunkModules = Object.create(null);
     for (const {
       dependentEntries,
       modules
     } of modulesWithDependentEntries) {
       let chunkSignature = 0n;
       for (const entryIndex of dependentEntries) {
         chunkSignature |= 1n << BigInt(entryIndex);
       }
       (chunkModules[String(chunkSignature)] ||= {
         dependentEntries: new Set(dependentEntries),
         modules: []
       }).modules.push(...modules);
     }
     return Object.values(chunkModules);
   }

   Brief Explanation

   BigInt is a data type in JavaScript used to represent arbitrarily large integers. In JavaScript, the maximum integer that can be represented by the Number type is 2^53 - 1 (i.e., 9007199254740991), while BigInt can represent arbitrarily large integers. chunkSignature is of type BigInt, where each bit represents an entry module in allEntries.

   • ModuleX has only one entry module 0, so its chunkSignature is 1n (i.e., 01)
   • ModuleA has only one entry module 0, so its chunkSignature is 1n (i.e., 01)
   • ModuleB has two entry modules 0 and 1, so its chunkSignature is 1n | 2n = 3n (i.e., 11)
   • ModuleH has only one entry module 4, so its chunkSignature is 16n (i.e., 10000)

   From this, we can see that ModuleX and ModuleA have the same chunkSignature, indicating they can be merged into the same chunk.

   Therefore, we can finally get:

   const chunkAtoms = [
     {
       dependentEntries: new Set([0]),
       modules: [ModuleX, ModuleA]
     },
     {
       dependentEntries: new Set([1]),
       modules: [ModuleY]
     },
     {
       dependentEntries: new Set([0, 1]),
       modules: [ModuleB]
     },
     {
       dependentEntries: new Set([3]),
       modules: [ModuleE]
     },
     {
       dependentEntries: new Set([4]),
       modules: [ModuleH]
     }
   ];

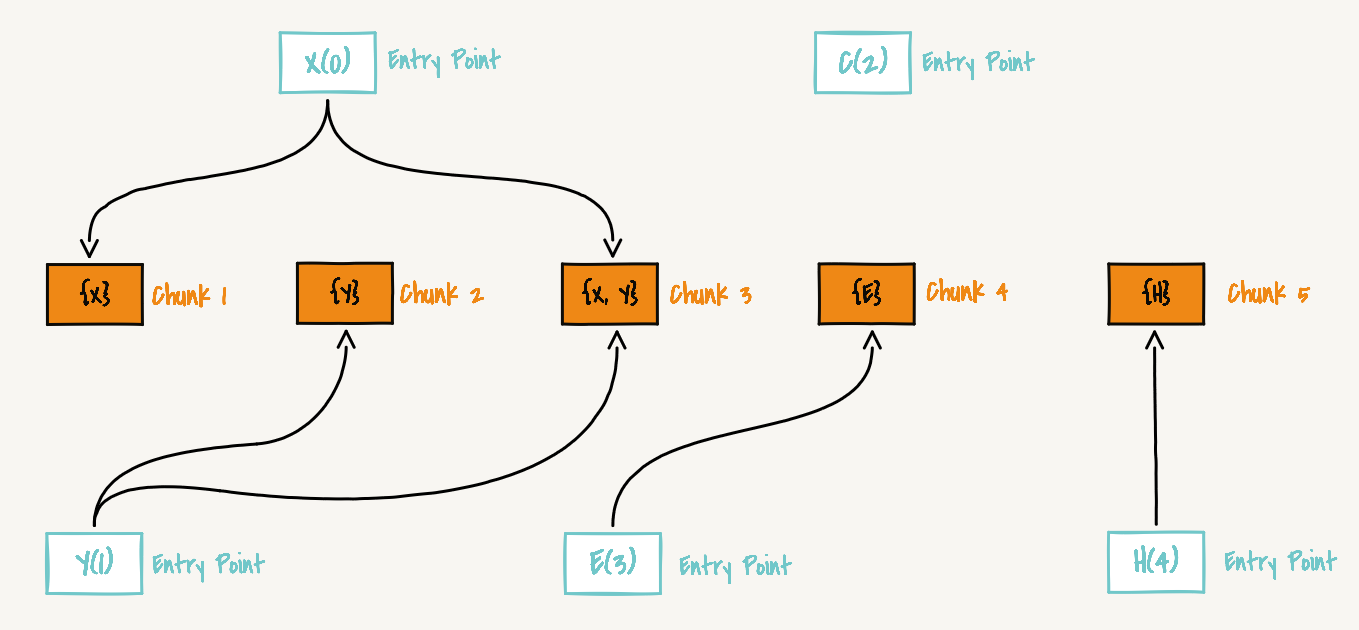
Counting Relationships Between Entry Modules and Associated Chunks

Through the processed chunkAtoms and allEntries, we can obtain the staticDependencyAtomsByEntry structure.

const staticDependencyAtomsByEntry = [5n, 6n, 0n, 8n, 16n];

Brief Explanation

This is a summary of chunkAtoms, creating a mapping relationship between entry modules and their associated chunks.

ModuleX's associated chunks include the first and third chunks in chunkAtoms.

First chunk:

{
  dependentEntries: new Set([0]),
  modules: [ModuleX, ModuleA]
}

Third chunk:

{
  dependentEntries: new Set([0, 1]),
  modules: [ModuleB]
}

So ModuleX's associated chunks can be represented as 5n (i.e., 101). We can easily derive the associated chunks for each entry dependency module, which we'll visualize below.

Dependency Graph Visualization:

Counting Already Loaded chunks During Dynamic Dependency Loading

alreadyLoadedAtomsByEntry is the approach for handling dynamic dependencies. We know that dynamic dependencies are loaded asynchronously, so normally when loading a dynamic dependency, the current static module has already been loaded. This is used to count which chunks have already been loaded when the current dynamic dependency module is loaded.

const alreadyLoadedAtomsByEntry = [0n, 0n, 5n, 4n, 4n];

Brief Explanation

Through staticDependencyAtomsByEntry, we can get the following dependency graph (mapping relationship between entries and associated chunks)

1. ModuleC is loaded as a dynamic dependency in ModuleA, and ModuleA's dependent entry module is ModuleX. From the above dependency graph, we can see that ModuleX's associated chunks include the first and third chunks in chunkAtoms, so alreadyLoadedAtomsByEntry[2(ModuleC's entry module index)] = 5n (i.e., 101).

2. ModuleE is loaded as a dynamic dependency in ModuleB and ModuleY. ModuleB's dependent entry modules are ModuleX and ModuleY, and ModuleY's dependent entry module is ModuleY. From the above dependency graph, we can see that ModuleX's associated chunks include the first and third chunks in chunkAtoms, and ModuleY's associated chunks include the second and third chunks in chunkAtoms, so alreadyLoadedAtomsByEntry[3(ModuleE's entry module index)] = 5n (i.e., 101) & 6n (i.e., 110) = 4n (i.e., 100). The reason for using the & operator to calculate the intersection of the two sets is that when ModuleE is loaded, the chunks in the intersection must have already been loaded.

3. ModuleH is loaded as a dynamic dependency in ModuleC. ModuleC's dependent entry modules are ModuleY and ModuleC. From the above dependency graph, we can see that ModuleY's associated chunks are 6n, and ModuleC doesn't have any associated chunks, but from point 1, we know that when loading ModuleC, 5n (i.e., 101) has already been loaded, so alreadyLoadedAtomsByEntry[4(ModuleH's entry module index)] = 6n (i.e., 110) & 5n (i.e., 101) = 4n (i.e., 100).

Removing Unnecessary Dependent Entry Modules

Next, in the removeUnnecessaryDependentEntries method, we use alreadyLoadedAtomsByEntry to remove unnecessary dependent entry modules from chunkAtoms.

/**
 * This removes all unnecessary dynamic entries from the dependentEntries in its
 * first argument if a chunk is already loaded without that entry.
 */
function removeUnnecessaryDependentEntries(
  chunkAtoms,
  alreadyLoadedAtomsByEntry
) {
  // Remove entries from dependent entries if a chunk is already loaded without
  // that entry.
  let chunkMask = 1n;
  for (const { dependentEntries } of chunkAtoms) {
    for (const entryIndex of dependentEntries) {
      if (
        (alreadyLoadedAtomsByEntry[entryIndex] & chunkMask) ===
        chunkMask
      ) {
        dependentEntries.delete(entryIndex);
      }
    }
    chunkMask <<= 1n;
  }
}

This means that if chunk A's dependent entry module is already loaded when the current chunk is loaded, then we delete the current chunk's dependent entry module A. Essentially, this handles circular dependency cases by removing duplicate dependent entry modules.

// Entry Module A
console.log('ModuleA');
import('./ModuleA_B').then(() => {
  console.log('Dynamic Module A_B');
});

// Entry Module B
console.log('ModuleB');
import('./ModuleA_B').then(() => {
  console.log('Dynamic Module A_B');
});

// Dynamic Entry Module A_B
import './ModuleA';
console.log('Dynamic Module A_B');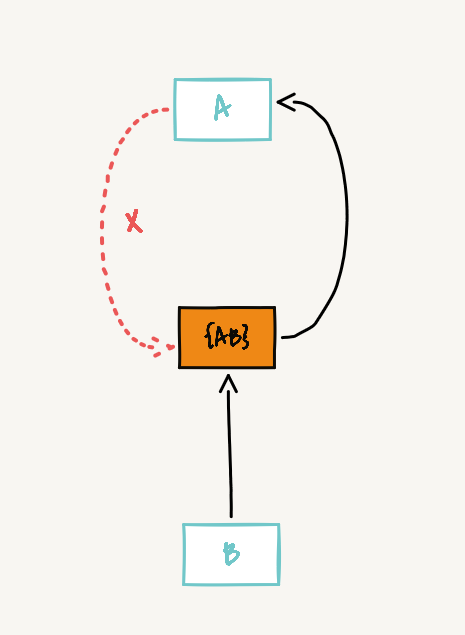

Building Chunks

Next, we generate the final chunks through the getChunksWithSameDependentEntriesAndCorrelatedAtoms method.

function getChunksWithSameDependentEntriesAndCorrelatedAtoms(
  chunkAtoms,
  staticDependencyAtomsByEntry,
  alreadyLoadedAtomsByEntry,
  minChunkSize
) {
  const chunksBySignature = Object.create(null);
  const chunkByModule = new Map();
  const sizeByAtom = [];
  let sideEffectAtoms = 0n;
  let atomMask = 1n;
  for (const { dependentEntries, modules } of chunkAtoms) {
    let chunkSignature = 0n;
    let correlatedAtoms = -1n;
    for (const entryIndex of dependentEntries) {
      chunkSignature |= 1n << BigInt(entryIndex);
      // Correlated atoms are the atoms that are guaranteed to be loaded as
      // well when a given atom is loaded. It is the intersection of the already
      // loaded modules of each chunk merged with its static dependencies.
      correlatedAtoms &=
        staticDependencyAtomsByEntry[entryIndex] |
        alreadyLoadedAtomsByEntry[entryIndex];
    }
    const chunk = (chunksBySignature[String(chunkSignature)] ||= {
      containedAtoms: 0n,
      correlatedAtoms,
      dependencies: new Set(),
      dependentChunks: new Set(),
      dependentEntries: new Set(dependentEntries),
      modules: [],
      pure: true,
      size: 0
    });
    let atomSize = 0;
    let pure = true;
    for (const module of modules) {
      // Mapping relationship between module and chunk
      chunkByModule.set(module, chunk);
      // Unfortunately, we cannot take tree-shaking into account here because
      // rendering did not happen yet, but we can detect empty modules
      if (module.isIncluded()) {
        pure &&= !module.hasEffects();
        // we use a trivial size for the default minChunkSize to improve
        // performance
        atomSize += minChunkSize > 1 ? module.estimateSize() : 1;
      }
    }
    if (!pure) {
      // Record that the current module has side effects
      sideEffectAtoms |= atomMask;
    }
    // Count the size of each chunk's modules
    sizeByAtom.push(atomSize);
    chunk.containedAtoms |= atomMask;
    chunk.modules.push(...modules);
    // Record whether the current chunk has side effects
    chunk.pure &&= pure;
    // Record the size of the current chunk's modules
    chunk.size += atomSize;
    atomMask <<= 1n;
  }
  const chunks = Object.values(chunksBySignature);
  sideEffectAtoms |= addChunkDependenciesAndGetExternalSideEffectAtoms(
    chunks,
    chunkByModule,
    atomMask
  );
  return { chunks, sideEffectAtoms, sizeByAtom };
}

In addChunkDependenciesAndGetExternalSideEffectAtoms, we implement the functionality of creating the chunk dependency graph and counting external module side effects.

function addChunkDependenciesAndGetExternalSideEffectAtoms(
  chunks,
  chunkByModule,
  nextAvailableAtomMask
) {
  const signatureByExternalModule = new Map();
  // Count side effects of external dependency modules
  let externalSideEffectAtoms = 0n;
  for (const chunk of chunks) {
    const { dependencies, modules } = chunk;
    for (const module of modules) {
      for (const dependency of module.getDependenciesToBeIncluded()) {
        if (dependency instanceof ExternalModule) {
          if (dependency.info.moduleSideEffects) {
            const signature = getOrCreate(
              signatureByExternalModule,
              dependency,
              () => {
                const signature = nextAvailableAtomMask;
                nextAvailableAtomMask <<= 1n;
                externalSideEffectAtoms |= signature;
                return signature;
              }
            );
            chunk.containedAtoms |= signature;
            chunk.correlatedAtoms |= signature;
          }
        } else {
          // Build chunk dependency graph
          const dependencyChunk = chunkByModule.get(dependency);
          if (dependencyChunk && dependencyChunk !== chunk) {
            chunk.dependencies.add(dependencyChunk);
            dependencyChunk.dependentChunks.add(chunk);
          }
        }
      }
    }
  }
  return externalSideEffectAtoms;
}

Optimizing Chunks

Further, we optimize chunks through the getOptimizedChunks method.

function compareChunkSize({ size: sizeA }, { size: sizeB }) {
  return sizeA - sizeB;
}
function getPartitionedChunks(chunks, minChunkSize) {
  const smallChunks = [];
  const bigChunks = [];
  for (const chunk of chunks) {
    (chunk.size < minChunkSize ? smallChunks : bigChunks).push(chunk);
  }
  if (smallChunks.length === 0) {
    return null;
  }
  // Sort from smallest to largest
  smallChunks.sort(compareChunkSize);
  bigChunks.sort(compareChunkSize);
  return {
    big: new Set(bigChunks),
    small: new Set(smallChunks)
  };
}
function getOptimizedChunks(
  chunks,
  minChunkSize,
  sideEffectAtoms,
  sizeByAtom,
  log
) {
  timeStart('optimize chunks', 3);
  const chunkPartition = getPartitionedChunks(chunks, minChunkSize);
  if (!chunkPartition) {
    timeEnd('optimize chunks', 3);
    return chunks; // the actual modules
  }
  if (minChunkSize > 1) {
    log(
      'info',
      parseAst_js.logOptimizeChunkStatus(
        chunks.length,
        chunkPartition.small.size,
        'Initially'
      )
    );
  }
  mergeChunks(chunkPartition, minChunkSize, sideEffectAtoms, sizeByAtom);
  if (minChunkSize > 1) {
    log(
      'info',
      parseAst_js.logOptimizeChunkStatus(
        chunkPartition.small.size + chunkPartition.big.size,
        chunkPartition.small.size,
        'After merging chunks'
      )
    );
  }
  timeEnd('optimize chunks', 3);
  return [...chunkPartition.small, ...chunkPartition.big];
}

This involves the chunk merging algorithm.

Chunk Merging Algorithm

General Introduction

• Dependent Entry Points: The entry module set that loads to the current module along the dependency path is the dependent entry points of the current module.
• Side Effects
  • Refers to operations that may affect global state, such as global function calls, global variable modifications, or potential errors.
  • The algorithm divides code blocks into pure (no side effects) and impure (has side effects).
• Correlated Side Effects:
  • All side effects that must have been triggered when loading a code block.
  • Is the intersection of all chunks loaded by entry points that depend on this code block.
• Dependent Side Effects:
  • Side effects triggered when directly loading a code block.
  • Includes the side effects of the code block itself and its direct dependencies.

For example:

In the above graph:

• X and Y are entry points
• Red blocks (A, B, D, F, G, H) represent code blocks with side effects
• Green blocks (C, E) represent pure code blocks (no side effects)

Now, let's analyze the correlated side effects of code block A:

1. A's Dependent Entry Points:

   • A can be loaded through entry point X or Y. So A's dependent entry points are ({X, Y}).

2. Determining Correlated Side Effects:

   • When loading A through X, it loads: A, B, C, F, G
   • When loading A through Y, it loads: A, D, E, F, H

3. Calculating Correlated Side Effects:

   • A's correlated side effects are the set of code blocks with side effects that appear in any possible loading path (X or Y).
   • This is the intersection of the two loading paths above: ({A, F}).

Therefore, A's correlated side effects are ({A, F}). This means that whenever A is loaded, F must also be loaded, and their side effects must be triggered.

1. Algorithm Goal: Try to eliminate small code blocks by merging them into other code blocks.

2. Safety Considerations for Merging: Merging must ensure that side effects that shouldn't be triggered (global function calls, global variable modifications, or potential errors, etc.) are not triggered.

3. Merging Rules:

   1. If code block A's dependent side effects are a subset of another code block B's correlated side effects, they can be merged.
   2. If code block A's dependent entry points are a subset of code block B's, and A's dependent side effects are a subset of B's correlated side effects, they can be merged.

4. Two Phases of the Merging Algorithm

   1. First Round:
      • Try to merge small code block A into another code block B, on the condition that A's dependent entry points are a subset of B's, and A's dependent side effects are a subset of B's correlated side effects.
   2. Second Round:
      • For remaining small code blocks, look for any merging opportunities that follow rule (3-1), starting from the smallest code block.

5. Additional Considerations

   When merging, we also need to consider avoiding loading too much additional code. Ideally, the small code block's dependent entry points are a subset of another code block's dependent entry points, which ensures that when loading the small code block, the other code block is already in memory.

Let's analyze the following example:

1. Code Block Definitions:

   • A, B, D, F: Have side effects
   • C, E: Pure code blocks (no side effects)

2. Dependency Relationships:

   • X -> A, B, C
   • Y -> A, D, E
   • A -> F

Now, let's analyze each code block's related concepts:

1. A:

   • Dependent Entry Points: {X, Y}
   • Correlated Side Effects: {A, F}
   • Dependent Side Effects: {A, F}

2. B:

   • Dependent Entry Points: {X}
   • Correlated Side Effects: {B}
   • Dependent Side Effects: {B}

3. C:

   • Dependent Entry Points: {X}
   • Correlated Side Effects: {} (pure code block)
   • Dependent Side Effects: {}

4. D:

   • Dependent Entry Points: {Y}
   • Correlated Side Effects: {D}
   • Dependent Side Effects: {D}

5. E:

   • Dependent Entry Points: {Y}
   • Correlated Side Effects: {} (pure code block)
   • Dependent Side Effects: {}

6. F:

   • Dependent Entry Points: {X, Y} (because A depends on F, and both X and Y depend on A)
   • Correlated Side Effects: {A, F}
   • Dependent Side Effects: {F}

Now, let's consider possible merges:

1. Merging F into A:

   • Can be safely merged, because F's dependent entry points ({X, Y}) are the same as A's dependent entry points ({X, Y})
   • F's dependent side effects ({F}) are a subset of A's correlated side effects ({A, F})

2. Merging B into A:

   • Cannot be safely merged, because although B's dependent entry points ({X}) are a subset of A's dependent entry points ({X, Y})
   • B's dependent side effects ({B}) are not a subset of A's correlated side effects ({A, F})

3. Merging C into B:

   • Can be safely merged, because C's dependent entry points ({X}) are the same as B's dependent entry points ({X})
   • C is a pure code block with no side effects, so its dependent side effects ({}) must be a subset of B's correlated side effects ({B})

4. Merging E into D:

   • Can be safely merged, for similar reasons as merging C into B

5. Merging D into A:

   • Cannot be safely merged, because although D's dependent entry points ({Y}) are a subset of A's dependent entry points ({X, Y})
   • D's dependent side effects ({D}) are not a subset of A's correlated side effects ({A, F})

Merge Results:

1. We can safely merge F into A, because F is always loaded with A, and F's side effects are already included in A's correlated side effects.
2. We can safely merge C into B, and E into D, because they are pure code blocks that won't introduce new side effects.
3. We cannot merge B or D into A, because this might incorrectly trigger B or D's side effects in scenarios where only A is needed.

Summary

Typically, the algorithm attempts to optimize overall loading performance by intelligently merging small code blocks while ensuring application correctness (especially regarding side effects).

::: </rewritten_file>

Contributors

XiSenao

Changelog

Last edited 21 days ago

View full history

9ba4ed7-feat: i18n

a989f82-chore: format code

eaafd87-chore: reformatting global code

4daa489-chore: prepare for the upcoming article on Rollup that you are going to write

286984d-doc: rollup generate chunks